Answers
Given:-
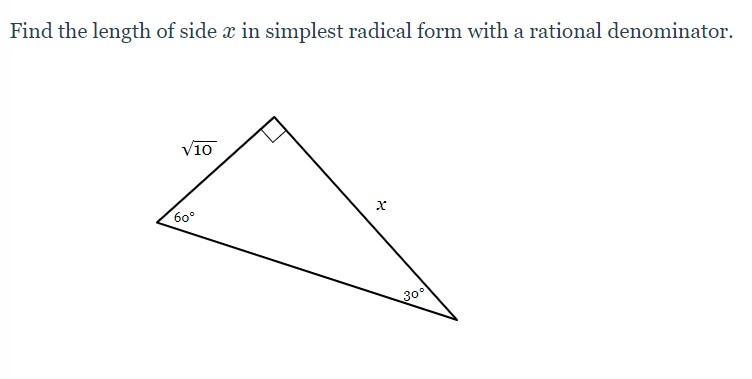
A right angled triangle with two angles 60° and 30° is given to us.Length of two shorter sides is x and √10 .To find:-
The value of x .Answer:-
Here since the given triangle is a right angled triangle, we may use the trigonometric ratios . We can see that perpendicular and base are involved in this question whose measures are "x" and "√10" respectively with respect to 60° angle. So here we may use the ratio of tangent as , in any right angled triangle,
[tex]\implies\tan\theta =\dfrac{p}{b} \\[/tex]
and here p = x , and b = √10 . So on substituting the respective values, we have;
[tex]\implies \tan\theta = \dfrac{x}{\sqrt{10}} \\[/tex]
Also the angle here is 60° , so that;
[tex]\implies\tan60^o =\dfrac{x}{\sqrt10} \\[/tex]
The value tan60° is √3 , so we have;
[tex]\implies \sqrt3 =\dfrac{x}{\sqrt10}\\[/tex]
[tex]\implies x =\sqrt{10}\cdot \sqrt{3}\\[/tex]
[tex]\implies x =\sqrt{10\cdot 3} \\[/tex]
[tex]\implies x =\sqrt{30} \\[/tex]
The value of √30 is approximately 5.48 , so that;
[tex]\implies \underline{\underline{\red{\quad x = 5.48\quad }}} \\[/tex]
Therefore the value of x is approximately 5.48 .
Answer:
The length of side x in simplest radical form is [tex]\sqrt{30}[/tex].
Step-by-step explanation:
From inspection of the given right triangle, we can see that the interior angles are 30°, 60° and 90°. Therefore, this triangle is a 30-60-90 triangle.
A 30-60-90 triangle is a special right triangle where the measures of its sides are in the ratio 1 : √3 : 2. Therefore, the formula for the ratio of the sides is b: b√3 : 2b where:
b is the shortest side opposite the 30° angle.b√3 is the side opposite the 60° angle.2b is the longest side (hypotenuse) opposite the right angle.We have been given the side opposite the 30° angle, so:
[tex]\implies b=\sqrt{10}[/tex]
The side labelled "x" is the side opposite the 60° angle, so:
[tex]\implies x=b\sqrt{3}[/tex]
Substitute the found value of b into the equation for x:
[tex]\implies x=\sqrt{10}\sqrt{3}[/tex]
[tex]\textsf{Apply the radical rule:} \quad \sqrt{a}\sqrt{b}=\sqrt{ab}[/tex]
[tex]\implies x=\sqrt{10 \cdot3}[/tex]
[tex]\implies x=\sqrt{30}[/tex]
Therefore, the length of side x in simplest radical form is [tex]\sqrt{30}[/tex].
[tex]\hrulefill[/tex]
We can also calculate the length of side x using the tangent trigonometric ratio:
[tex]\boxed{\tan \theta=\sf \dfrac{O}{A}}[/tex]
where:
θ is the angle.O is the side opposite the angle.A is the side adjacent the angle.From inspection of the given right triangle:
θ = 30°O = √(10)A = xSubstitute these values into the formula:
[tex]\implies \tan 30^{\circ}=\dfrac{\sqrt{10}}{x}[/tex]
[tex]\implies \dfrac{\sqrt{3}}{3}=\dfrac{\sqrt{10}}{x}[/tex]
[tex]\implies x\sqrt{3}=3\sqrt{10}[/tex]
[tex]\implies x=\dfrac{3\sqrt{10}}{\sqrt{3}}[/tex]
Rationalise the denominator by multiplying the numerator and denominator by √3:
[tex]\implies x=\dfrac{3\sqrt{10}}{\sqrt{3}}\cdot \dfrac{\sqrt{3}}{\sqrt{3}}[/tex]
[tex]\implies x=\dfrac{3\sqrt{10}\sqrt{3}}{3}[/tex]
[tex]\implies x=\sqrt{10}\sqrt{3}[/tex]
[tex]\implies x=\sqrt{10\cdot3}[/tex]
[tex]\implies x=\sqrt{30}[/tex]
Therefore, the length of side x in simplest radical form is [tex]\sqrt{30}[/tex].
Related Questions
View the photo and solve the probability
Answers
Therefore, the probability that at least one of the next six births is a girl is 1 - 0.033 = 0.967 (rounded to three decimal places).
What is Probability?Probability is a measure of the likelihood that an event will occur. It is a number between 0 and 1, with 0 indicating that the event is impossible and 1 indicating that the event is certain.
To calculate the probability of an event, you divide the number of ways that event can occur by the total number of possible outcomes. For example, if you flip a fair coin, there are two possible outcomes - heads or tails - and each has an equal probability of 0.5 (or 50%) of occurring.
Given by the question.
To find the probability that at least one of the next six births is a girl, we can find the probability that all six of them are boys and subtract it from 1.
The probability that one birth is a girl is 1 - 0.513 = 0.487.
The probability that all six births are boys is. [tex]0.513^{6}[/tex] = 0.033.
To learn more about probability:
https://brainly.com/question/30034780
#SPJ1
which is more 7,000 millimeters or 7 liters?
Answers
A,B and B,C form a right angle at point B. If A = (-3,-1) and B = (4,4), what is the equation of B,C?
Answers
Answer:
the equation of line BC is y = (-7/5)x + (48/5).
Step-by-step explanation:
To find the equation of the line that passes through points B and C, we first need to determine the coordinates of point C. Since the angle at B is a right angle, we can use the slope of line AB to find the slope of line BC.
The slope of line AB is:
mAB = (yB - yA) / (xB - xA)
= (4 - (-1)) / (4 - (-3))
= 5/7
Since lines AB and BC are perpendicular, the slope of line BC is the negative reciprocal of the slope of line AB:
mBC = -1 / mAB
= -7/5
Now we can use the point-slope form of the equation of a line to find the equation of line BC. We can use point B as the known point, since we already know its coordinates:
y - yB = mBC(x - xB)
Substituting the values we have:
y - 4 = (-7/5)(x - 4)
Expanding and simplifying:
y - 4 = (-7/5)x + (28/5)
y = (-7/5)x + (48/5)
Problem 13 and problem 20 ?
Answers
The answers to both questions are as:
(a) the value of the investment after 5 years is $14,917.95, after 10 years is $23,673.58, and after 15 years is $37,337.35,
b) the amount of the final payment is $688.32.
What is compound interest?
Compound interest is when you earn interest on both the money you've saved and the interest you earn.
We can use the formula for compound interest to solve this problem:
[tex]A = P(1 + r/n)^{(nt)}[/tex]
where A is the final amount, P is the principal (initial investment), r is the annual interest rate (as a decimal), n is the number of times the interest is compounded per year, and t is the time (in years).
(a) For 5 years with semiannual compounding:
n = 2 (compounded semiannually)
r = 0.08 (8% annual rate)
t = 5
[tex]A = 9900(1 + 0.08/2)^{(2*5)}[/tex]
A = $14,917.95
(b) For 10 years with semiannual compounding:
n = 2 (compounded semiannually)
r = 0.08 (8% annual rate)
t = 10
[tex]A = 9900(1 + 0.08/2)^{(2*10)}[/tex]
A = $23,673.58
(c) For 15 years with semiannual compounding:
n = 2 (compounded semiannually)
r = 0.08 (8% annual rate)
t = 15
[tex]A = 9900(1 + 0.08/2)^{(2*15)}[/tex]
A = $37,337.35
Therefore, the value of the investment after 5 years is $14,917.95, after 10 years is $23,673.58, and after 15 years is $37,337.35, assuming the interest is compounded semiannually.
To calculate the final payment, we can first find the balance of the loan at the end of the fifth year, and then use this as the principal to calculate the balance at the end of the tenth year.
The interest rate is 5% per year, compounded quarterly. This means that the quarterly interest rate is:
r = 5% / 4 = 0.0125
Let B be the balance of the loan after 5 years. Then we have:
B = 1000*(1 + r)²⁰- 200*(1 + r)⁴
where the first term is the future value of the initial loan after 5 years, and the second term is the present value of the first payment of $200.
Plugging in the values, we get:
B = 1000*(1 + 0.0125)²⁰ - 200*(1 + 0.0125)⁴
B = 1000*(1.0125)²⁰ - 200*(1.0125)⁴
B = 1346.49
So the balance of the loan after 5 years is $1346.49. We can use this as the principal to calculate the balance at the end of the tenth year, which is the final payment we are looking for.
Let P be the final payment. Then we have:
P = 1346.49*(1 + r)⁴⁰ - 800*(1 + r)²⁰
where the first term is the future value of the balance after 10 years, and the second term is the present value of the second payment of $800.
Plugging in the values, we get:
P = 1346.49*(1 + 0.0125)⁴⁰ - 800*(1 + 0.0125)²⁰
P = 1346.49*(1.0125)⁴⁰ - 800*(1.0125)²⁰
P = 688.32
So the amount of the final payment is $688.32.
hence, the answers to both questions are as:
(a) the value of the investment after 5 years is $14,917.95, after 10 years is $23,673.58, and after 15 years is $37,337.35,
b) the amount of the final payment is $688.32.
To learn more about compound interest visit:
https://brainly.com/question/3989769
#SPJ1
A school gym is 97 feet long and 61 feet wide. What is its perimeter?
Answers
Answer:
316
Step-by-step explanation:
in square abcd, BE=13 find BC
Answers
Answer:
13sqrt{2}
Step-by-step explanation:
let's assume one side of square is a;
diognal which is BD=
[tex]a\sqrt{2}\\BE is BD/2=\frac{a\sqrt{2}}{2}=13\\a\sqrt{2}=26\\a=26/\sqrt{2}=13\sqrt{2}[/tex]
BC=CD=DA=AB=a=13sqrt{2}
A prism is completely filled with 96 cubes that have edge length of 1/2 cm.
What is the volume of the prism?
Thank you for answering ⋄∵₊⁺⧭ʷ⧬⁺₊∵⋄
Answers
Answer:
Since the prism is completely filled with 96 cubes that have an edge length of 1/2 cm, we can find the volume of the prism by multiplying the number of cubes by the volume of each cube.
The volume of each cube is (1/2 cm)^3 = 1/8 cm^3.
The number of cubes is 96.
Therefore, the volume of the prism is:
volume = (number of cubes) x (volume of each cube)
volume = 96 x (1/8 cm^3)
volume = 12 cm^3
So, the volume of the prism is 12 cubic centimeters.
there are 4 types of ice cream, 3 different cones and 3 choices of toppings. how many different ways can an ice cream cone be ordered
Answers
Answer:
25
Step-by-step explanation:
SOMEONE PLEASE HELP ME!!
Answers
Measure of the arc or angle indicated is 150.9 degrees.
Describe Arc?In geometry, an arc is a portion of the circumference of a circle or any other curved shape. It is defined by two endpoints and all the points on the curve that lie between them. An arc is usually named by its two endpoints, with a small arc symbol above them to indicate that it is an arc.
The length of an arc can be calculated using the formula:
Arc length = (central angle/360) x 2πr
where r is the radius of the circle, and the central angle is the angle subtended by the arc at the center of the circle, measured in degrees.
The measure of an arc is the degree measure of the central angle subtended by the arc. A semicircle is an arc that subtends a central angle of 180 degrees, and a full circle is an arc that subtends a central angle of 360 degrees.
Since DE and PE are chords of the circle, and they intersect at point P, we can use the intersecting chords theorem to find the length of DP. Let x be the length of DP. Then:
DP * PE = DE * PC
x * (x + PE) = ([tex]\frac{CE}{2}[/tex]) * ([tex]\frac{CE}{2}[/tex])
x² + x(PE) - [tex]\frac{CE}{2}^{\frac{2}{4} }[/tex] = 0
Since angle DPE is 60 degrees, we can use the law of cosines to find PE. Let y be the length of PE. Then:
y² = DE² + DP² - 2 * DE * DP * cos(60)
y² = ([tex]\frac{CE}{2}[/tex])² + x^2 - ([tex]\frac{CE}{2}[/tex]) * x
Substitute this expression for y^2 into the equation for x and simplify:
[tex]x^{2} +x((\frac{CE}{2})^{2} + x^{2} -\frac{CE}{2} *x)^{0.5} -(\frac{CE}{2} ^{\frac{2}{4} } )=0[/tex]
Solve for x:
x = [tex]\frac{CE^{2} -4*(CE^{2} -3*\frac{CE}{2} ^{2} )^{0.5} }{4}[/tex]
x = [tex]\frac{3}{4} *\frac{CE^{2} }{CE^{2} -12}[/tex]
Now we can find the measure of the CD arc by using the formula for the central angle:
CD arc = [tex]2*arctan(\frac{DP}{CE})[/tex]
CD arc = [tex]2*arctan(\frac{x}{\frac{CE}{2} } )[/tex]
CD arc = [tex]2* arctan(CE^{2} -4*(CE^{2} -3*\frac{(\frac{CE}{2} ^{2})^{0.5}}{CE^{2}-12 } ))[/tex]
Simplifying this expression, we get:
[tex]CD arc=2*arctan(2*3^{\frac{1}{2} } -1)[/tex]
CD arc ≈ 150.9 degrees.
To know more about expression visit:
https://brainly.com/question/10063670
#SPJ1
Measure of the arc or angle indicated in the given figure is 150.9 degrees.
Describe Arc?In geometry, an arc is a portion of the circumference of a circle or other curved shape. It is defined by his two endpoints and all midpoints of the curve. Arcs are usually named after their two endpoints, with a small arc symbol above them to indicate that they are arcs.
Arc Length = (Center Angle/360) x 2πr
where r is the radius of the circle and the central angle is the angle the arc makes at the center of the circle, measured in degrees.
The arc measurement is the angle of the central angle defined by the arc. A half circle is an arc that spans a central angle of 180 degrees, and a full circle is an arc that spans a central angle of 360 degrees.
Since DE and PE are chords of the circle and intersect at P, we can use the chord rule to find the length of DP. Let x be the length of DP. Then:
DP × PE = DE × PC
x × (x + PE) = (CE/2) × (CE/2)
x² + x(PE) - [tex]\frac{CE}{2} ^{\frac{2}{4} }[/tex] = 0
Since angle DPE is 60 degrees, we can use the law of cosines to find PE. Let y be the length of PE. Then:
y² = DE² + DP² - 2 × DE × DP × cos(60)
y² = ([tex]\frac{CE}{2}[/tex])² + x² - ([tex]\frac{CE}{2}[/tex]) × x
Substitute this expression for y² into the equation for x and simplify:
[tex]x^{2} +x((\frac{CE}{2} ^{2}) + x^{2} - \frac{CE}{2}*x)^{0.5} -[/tex] [tex]\frac{CE}{2} ^{\frac{2}{4} }[/tex] = 0
Solve for x:
x = [tex]\frac{CE^{2} - 4*(CE^{2}-3*\frac{CE}{2} ^{2})^{0.5} }{4}[/tex]
x = (3/4) × (CE²/CE²-12)
Now we can find the measure of the CD arc by using the formula for the central angle:
CD arc = 2arc tan(DP/CE)
CD arc = 2arc tan [x/(CE/2)]
CD arc = 2arc tan (CE² - 4 × (CE² - 3 × [tex]\frac{(\frac{CE}{2} ^{2}) ^{0.5} }{CE^{2}-12 }[/tex] )
Simplifying this expression, we get:
CD arc ≈ 150.9 degrees.
To know more about arc, visit:
https://brainly.com/question/16930503
#SPJ1
Solve for x. Round to the nearest tenth.
x =
(35 points)
Answers
The value of x rounded to the nearest tenth is equal to 24.3 units.
How to determine the value of x?In order to determine the value of x, we would apply basic trigonometry. From the information provided about this right angled triangle, we can logically deduce the following parameters:
Adjacent side (Adj) = xHypotenuse (Hyp) = 26.Angle = 21 degrees.Therefore, we would use the cosine trigonometry to determine the value of x as follows:
Cosθ = Adj/Hyp
Cos21 = x/26
x = 26cos21
x = 26(0.9336)
x = 24.3 units.
Read more on trigonometry here: brainly.com/question/26964482
#SPJ1
Use the quadratic formula to solve the equation 2 - 5x-9=0
Answers
The answer is x = 5±√61/2, I really hope this helps (:
please help image attached! x=?
Answers
Answer:
90°
Step-by-step explanation:
from the figure and the measurements it is a square, the diagonals are perpendicular and form 4 angles of 90°, so 90° is your answer.
3% of a sum of money is $60.What is the sum of money?
Answers
Answer:
2000
Step-by-step explanation:
Formula = Number x 100/Percent = 600 x 100/3 = 2,000
Following shows the steps on how to derive this formula and find out 3% of what number is 60.
Step 1: If 3% of a number is 60, then what is 100% of that number? Setup the equation.
60/3% = Y/100%
Step 2: Solve for Y
Using cross multiplication of two fractions, we get
3Y = 60 x 100
3Y = 6000
Y = 6000/100= 2000
Got it right already
Find the annual percentage rate for an account earning compound interest at a rate of 3.425%
Complete the table to find the APR when compounded semiannually and quarterly.
Answers
The APR when compounded semiannually and quarterly would be :
Compounded semi - annually - (1.034543) ^ t - 3.4543%Compounded quarterly - (1.034692) ^ t - 3.4692%How to find the APR ?To find the APR when compounded semi - annually, we first need to find the periodic rate to be :
= Annual rate / 2 semi annual periods
= 3. 425 / 2
= 1.7125%
Then use the Effective Annual Rate (EAR) to find the APR to be:
= ( 1 + periodic rate ) ^ number of periods - 1
= ( 1 + 1. 7125 % ) ² - 1
= 3.4543%
For the APR when compounding quarterly, you can variate the EAR formula to the original version of:
= ( 1 + annual rate / number of periods ) ^ number of periods - 1
= ( 1 + 3. 425 / 4 ) ⁴ - 1
= 3.4692%
Find out more on effective annual rate at https://brainly.com/question/13056587
#SPJ1
Easy (7th-grade math)
Answers
Answer:
384 cm
Step-by-step explanation:
hope this helps ! good luck on ur assignment! <3
13. The profit, in thousands of dollars, from the sale of x kilogram of coffee bean can be modelled by the function () = 5−400 +600 . a) State the asymptotes and the intercepts. Then, sketch a graph of this function using its key features. (5 pts) b) State the domain and range in this context. (2 points) c) Explain the significance of the horizontal asymptote. (1 point) d) Algebraically, find how much amount of tuna fish, in kg, should be sold to have a profit of exactly $4000? (4 points) SOLUTION
Answers
Answer: a) The profit function can be written as:
P(x) = 5x - 400x + 600
To find the asymptotes, we can look at the denominator of the second term, which is (x - 3). This means that there is a vertical asymptote at x = 3. To find the intercepts, we can set P(x) = 0:
5x - 400x + 600 = 0
Solving for x, we get:
x = 1.5 and x = 2.5
Therefore, there are x-intercepts at (1.5, 0) and (2.5, 0). To sketch the graph, we can also note that the coefficient of x^2 is negative, which means that the graph is a downward-facing parabola.
b) The domain of the function is the set of all possible values of x, which in this context represents the amount of coffee sold. Since we cannot sell a negative amount of coffee, the domain is x ≥ 0.
The range of the function is the set of all possible values of P(x), which represents the profit. Since the coefficient of x^2 is negative, the maximum profit occurs at the vertex of the parabola. The vertex has x-coordinate:
x = -b/(2a) = -(-400)/(2(-200)) = 1
Therefore, the maximum profit occurs when x = 1. The vertex has y-coordinate:
P(1) = 5(1) - 400(1) + 600 = 205
Since the coefficient of x^2 is negative, the range is (-∞, 205].
c) The horizontal asymptote of the function is y = -400, which represents the long-term average profit per kilogram of coffee sold. This means that as x gets very large, the profit per kilogram approaches -400. This could happen, for example, if the cost of producing the coffee increased significantly while the price remained the same.
d) To find the amount of coffee that must be sold to make a profit of $4000, we can set P(x) = 4000 and solve for x:
5x - 400x + 600 = 4000
Simplifying, we get:
-395x = -3400
Dividing both sides by -395, we get:
x ≈ 8.61
Therefore, approximately 8.61 kg of coffee must be sold to make a profit of $4000.
Step-by-step explanation:
Which of the following is the product of the rational expressions show below?
Answers
Answer:
−(3x2+−xx−5)
Step-by-step explanation:
Select the set of numbers that are arranged from greatest to least.
OA) 2.4 x 10; 2.7 x 105; 3.1 x 105
OB) 3.1 x 10; 2.4 x 10;
2.7 x 105
OC) 2.7 x 105;
2.4 x 10¹;
3.1 x 10¹
OD) 3.1 x 10³; 2.7 x 105;
2.4 x 10
Answers
The set of numbers arranged from greatest to least is:
OC) 2.7 x 105; 3.1 x 10¹; 2.4 x 10¹0
To see why, let's convert each number to scientific notation, which makes it easier to compare them:
OA) 2.4 x 10 = 24
2.7 x 105 = 270,000
3.1 x 105 = 310,000
OB) 3.1 x 10 = 31
2.4 x 10 = 24
2.7 x 105 = 270,000
OC) 2.7 x 105 = 270,000
2.4 x 10¹ = 24
3.1 x 10¹ = 31
OD) 3.1 x 103 = 3,100
2.7 x 105 = 270,000
2.4 x 10 = 24
As we can see, the set of numbers in option OC is arranged from greatest to least, with 2.7 x 105 being the largest number, followed by 3.1 x 10¹, and then 2.4 x 10¹0 as the smallest number
Polly's sister-in-law is going to have a baby! For the baby shower, Polly decided to sew pillow to give as a gift. She is using a flower-printed rectangular piece of fabric that is 26 inches long and 22 inches wide.
Answers
Answer:
The answer is 96
Step-by-step explanation:
2*(26+22)
2*48
96
I need help with my homework
Answers
To find the length of a line segment in a circle, use the formula [tex]d = 2r[/tex] [tex]sin(t/2)[/tex] , where r is the radius of the circle and t is the angle between the radii. The length of segment DE is [tex]5[/tex] units.
What is the formula for circle segment length?We can use the similar triangles property to find the missing length of segment DE in the given figure. Because triangles ABD and CBE are similar, we can use a proportion to find the length of DE:
[tex]CB/BE = AB/BD[/tex]
With the given values, we get:
[tex]3/6 = 5/(5 + DE)[/tex]
When we simplify and solve for DE, we get:
[tex]3(5 + DE) = 6 * 5 \s15 + 3DE = 30[/tex]
[tex]3DE = 15 \sDE = 5[/tex]
Therefore, segment DE has a length of 5 units.
Learn more about circle here:
https://brainly.com/question/28612561
#SPJ1
Complete the ratio table to convert the units of time from hours to weeks or weeks to hours.
Hours:
168 1 week
1,008. ____week
_____. 5 weeks
Answers
Answer:
6 weeks and 840 hours
Step-by-step explanation:
There are 168 hours in one week.
24 hrs/day * 7 days = 168 hours
1008 hours ÷ 24 hours(1 day) = 42 days ÷ 7 days in a week = 6 weeks
168 hours/week * 5 weeks = 840 hours
the cost for3.8 pounds of shrimp is 18.05 . find the unit price in dollars per pound. if necessary round it to the nearest cent
Answers
The unit price in dollars per pound is $4.75 (rounded to the nearest cent).
What is profit and loss?
Mathematicians use the profit and loss formula to calculate market prices for goods and to assess how lucrative a company is. There is a selling price and a cost price for every commodity. We can determine the profit made or loss suffered for a specific commodity based on the values of these prices. Cost price, fixed, variable, and semi-variable costs, selling price, marked price, list price, margin, etc. are some of the key words that are discussed in this article.
To find the unit price in dollars per pound, we need to divide the total cost by the total weight:
Unit price = Total cost / Total weight
In this case, the total weight is 3.8 pounds and the total cost is $18.05.
Unit price = $18.05 / 3.8 pounds
Unit price = $4.75 per pound (rounded to the nearest cent)
Therefore, the unit price in dollars per pound is $4.75 (rounded to the nearest cent).
Learn more about cost on:
https://brainly.com/question/19104371
#SPJ9
Write the polynomial in standard form. Then classify the polynomial by degree and by number of terms.
7x² +9x² - 6x²
Write the polynomial in standard form.
(Simplify your answer.)
Answers
Answer:
Step-by-step explanation:
When we combine like terms, we get:
7x² +9x² - 6x² = (7+9-6)x² = 10x²
So the polynomial in standard form is 10x².
The degree of the polynomial is 2 (since the highest power of the variable x is 2) and the number of terms is 1 (since there is only one term). Therefore, we classify this polynomial as a quadratic monomial.
Which of the following sets of numbers could represent the three sides of a
triangle?
{7, 15, 20}
{7, 16, 23}
O {11, 22, 35}
O {5, 17, 22}
Answers
The following sets of numbers could represent the three sides of a
triangle is {7, 15, 20}.
How to determine the set that represent the three sides of a triangleThe set of numbers {7, 15, 20} could represent the three sides of a triangle, but the other sets of numbers do not satisfy the triangle inequality theorem, which states that the sum of any two sides of a triangle must be greater than the third side. Checking the sets of numbers:
For {7, 15, 20}, 7 + 15 > 20, 7 + 20 > 15, and 15 + 20 > 7, so they satisfy the triangle inequality theorem and could represent the sides of a triangle.
For {7, 16, 23}, 7 + 16 < 23, so they do not satisfy the triangle inequality theorem and cannot represent the sides of a triangle.
For {11, 22, 35}, 11 + 22 < 35, so they do not satisfy the triangle inequality theorem and cannot represent the sides of a triangle.
For {5, 17, 22}, 5 + 17 < 22, so they do not satisfy the triangle inequality theorem and cannot represent the sides of a triangle.
Therefore, the answer is {7, 15, 20}.
Learn more about triangle at https://brainly.com/question/17335144
#SPJ1
please answer this question: the length of a rectangle is 6 centimeters less than its width. what are the dimensions of the rectangle if it's area is 160 square centimeters?
Answers
LW = 112
(W - 6)W = 112
W2 - 6W - 112 = 0
(W - 14)(W + 8) = 0
W = 14 cm
L = W - 6 = 14 - 6 = 8 cm
I Hope the helps. The answer is 8 cm.
Can someone help please
Answers
let's bear in mind that complex roots never come alone, their conjugate sister is always with her, so if we have the complex root of "i" or namely "0 + i", her conjugate is also coming along, or "0 - i", so we really have four roots, so
[tex]\begin{cases} x = 0+i &\implies x -i=0\\ x = 0-i &\implies x +i=0\\ x = \sqrt{2} &\implies x -\sqrt{2}=0\\ x = 3 &\implies x -3=0\\ \end{cases} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{original~polynomial}{a ( x -i )( x +i )( x -\sqrt{2} )( x -3 ) = \stackrel{0}{y}}\hspace{5em}\stackrel{\textit{we are assuming that}}{a=1} \\\\\\ 1( x -i )( x +i )( x -\sqrt{2} )( x -3 ) = y\implies ( x -i )( x +i )( x -\sqrt{2} )( x -3 ) = y \\\\[-0.35em] ~\dotfill[/tex]
[tex]\stackrel{ \textit{difference of squares} }{( x -i )( x +i )}\implies x^2 - i^2\implies x^2-(-1)\implies x^2+1 \\\\[-0.35em] ~\dotfill\\\\ (x^2+1)( x -\sqrt{2} )( x -3 )\implies (x^2+1)(x^2-3x-x\sqrt{2}+3\sqrt{2}) \\\\\\ (x^2+1)[x^2-x(3+\sqrt{2})+3\sqrt{2}] \\\\\\ x^4-x^3(3+\sqrt{2})+3x^2\sqrt{2}+x^2-x(3+\sqrt{2})+3\sqrt{2} \\\\\\ \boxed{x^4-x^3(3+\sqrt{2})+x^2(3\sqrt{2}+1)-x(3+\sqrt{2})+3\sqrt{2}~~ = ~~y}[/tex]
Which fraction is larger 3/4 or 1/4
Answers
Answer:
3/4
Step-by-step explanation:
3/4 is larger because since they have the same denominator (the bottom value), you compare the numerators (the top value). Whichever numerator is bigger gives you the larger fraction.
Answer: 3/4 is larger, this is simply because 3/4 is = 75%
whereas 1/4 = 25%
Y=4x+2 -6x+2y=8 what is the value x t y
Answers
Y = 4x + 2
-6x + 2y = 8
We can start by rearranging the second equation to solve for y:
-6x + 2y = 8
2y = 6x + 8
y = 3x + 4
Now we can substitute this expression for y into the first equation:
Y = 4x + 2
3x + 4 = 4x + 2
Subtracting 4x from both sides:
x = -2
To find the value of y, we can substitute x = -2 into either equation:
Y = 4x + 2
Y = 4(-2) + 2
Y = -6
Therefore, the solution to the system of equations is x = -2 and y = -6.
need statements 1 and 2 answered by Friday March 23, 2023 at 10am
Answers
I will give you some intuitive remarks for some inspiration on the proofs.
For the first one, notice that if m divides n then n = pm where p is a integer.
Since n and m are both natural numbers p then must be a natural number as well.
Now we know that basically we want to prove that if a is congruent to b mod n then a is congruent to b mod "a factor of n" (this is cause n = pm).
Tell me if you need more clarification.
For the second proof, I would just draw a Venn diagram and prove that the two intersections cover identical regions.
What is 7% as a decimal ?
Answers
Answer: 0.07%
Step-by-step explanation:
Answer:
0.07
Step-by-step explanation: